Cet article fournit le code d'une horloge analogique, programmée en Python, PyGObject et Cairo. On n'est plus ici dans le cas d'un exemple minimal : 250 lignes de code !

L'horloge est responsive, comme on dit dans le Berry, c'est-à-dire que les tailles s'adaptent aux dimensions de la fenêtre :

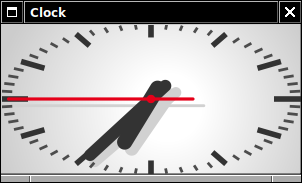
Elle s'intègre bien dans un dock :

Le design s'inspire de la célèbre horloge de gare des Chemins de fer Fédéraux Suisses (CFF ou SBB en allemand) créée en 1944, au moins pour les graduations et la couleur de l'aiguille des secondes :

Le modèle physique pour construire les ombres des aiguilles a été fait en quelques minutes sur un coin de table et il est assez primitif. Le résultat paraît convenable et je n'ai pas cherché plus loin.

Le code

#!/usr/bin/python
# jpsb le 9 août 2024
# Une horloge analogique en Python, PyGObject et Cairo
# licence : GPL 3

import gi
gi.require_version("Gtk", "3.0")
from gi.repository import Gtk, GLib
import math
import time
import cairo

class Clock(Gtk.Window):

    def __init__(self):
        super().__init__(title="Clock")

        # ~ self.resize(86, 86)
        self.resize(800, 800)
        self.connect("delete-event", Gtk.main_quit)

        # on crée la figure et on l'ajoute à la fenêtre
        self.darea = Gtk.DrawingArea()
        self.darea.connect("draw", self.on_draw)
        self.add(self.darea)

        # on shédule la prochaine mise à jour dans 1s
        GLib.timeout_add_seconds(1, self.on_timer)


    # fonction mise à jour du dessin
    def on_timer(self):

        self.darea.queue_draw()

        return True

    # fonction calcul distance
    def distance(self,x,y,xp,yp):
        return math.sqrt((x-xp)**2+(y-yp)**2)

    # fonction calcul d'angle (al-Kashi)
    def alpha(self,a,b,c):
        return math.acos((c**2+b**2-a**2)/(2*b*c))

    # tracé cairo de l'horloge
    def on_draw(self, wid, cr):

        # on récupère la taille de la fenêtre
        w=self.get_size().width
        h=self.get_size().height

        # on place l'origine du repère au centre
        cr.translate(w/2, h/2) 

        # réglages : longueurs, largeurs et couleurs
        r=math.sqrt((w/2)**2+(h/2)**2)
        l_grad_5 = 18/100
        l_grad = 7/100
        l_hour = 60/100
        l_min = 85/100
        l_sec = 95/100

        w_grad_5 = r/30
        w_grad = r/60
        w_hour = r/11
        w_minute = r/14
        w_second = r/53

        c_grad_5 = (.2,.2,.2)
        c_grad = (.3,.3,.3)
        c_hour = (.2,.2,.2)
        c_minute = (.2,.2,.2)
        c_second = (.9,.0,.1)
        c_shadow = (.82,.82,.82)

        # coordonnées lumière pour les ombres
        x_a=-w/2
        y_a=-h/2
        theta = math.atan(x_a/y_a)
        # hauteur des aiguilles
        k=.04*r

        # fond en dégradé
        cr.rectangle(-w/2, -h/2, w, h)
        r1 = cairo.RadialGradient(0.1*r, 0.05*r, 0.2*r, 0.05*r, 0.1*r, r)
        r1.add_color_stop_rgb(0, 1, 1, 1)
        r1.add_color_stop_rgb(1, .8, .8, .8)
        cr.set_source(r1)
        cr.fill()

        # recup de l'heure
        now = time.localtime()        
        hour = now.tm_hour % 12
        minute = now.tm_min
        second = now.tm_sec

        # calculs aiguille des heures et ombre
        hour_angle = (hour + minute/60) * math.pi/6 - math.pi/2
        hour_end_x = l_hour * w/2 * math.cos(hour_angle)
        hour_end_y = l_hour * h/2 * math.sin(hour_angle)
        hour_start_x = -0.15 * w/2 * math.cos(hour_angle)
        hour_start_y = -0.15 * h/2 * math.sin(hour_angle)

        ap=self.distance(0,0,hour_start_x,hour_start_y)
        op=self.distance(x_a,y_a,hour_start_x,hour_start_y)
        sp=self.distance(0,0,x_a,y_a)
        alpha_anglep=self.alpha(ap,sp,op)

        hour_shadow_start_x = hour_start_x + k*math.tan(theta-alpha_anglep)
        hour_shadow_start_y = hour_start_y + k
        a=self.distance(0,0,hour_end_x,hour_end_y)
        o=self.distance(x_a,y_a,hour_end_x,hour_end_y)
        e=self.distance(0,0,x_a,y_a)
        alpha_angle=self.alpha(a,o,e)

        hour_shadow_end_x = hour_end_x + k*math.tan(theta-alpha_angle)
        hour_shadow_end_y = hour_end_y + k

        # calculs aiguilles des minutes et ombre
        minute_angle = (minute + second/60) * math.pi/30 - math.pi/2
        minute_end_x = l_min * w/2 * math.cos(minute_angle)
        minute_end_y = + l_min * h/2 * math.sin(minute_angle)
        minute_start_x = -0.20 * w/2 * math.cos(minute_angle)
        minute_start_y = -0.20 * h/2 * math.sin(minute_angle)

        ap=self.distance(0,0,minute_start_x,minute_start_y)
        op=self.distance(x_a,y_a,minute_start_x,minute_start_y)
        sp=self.distance(0,0,x_a,y_a)
        alpha_anglep=self.alpha(ap,sp,op)

        minute_shadow_start_x = minute_start_x + k*math.tan(theta-alpha_anglep)
        minute_shadow_start_y = minute_start_y + k
        a=self.distance(0,0,minute_end_x,minute_end_y)
        o=self.distance(x_a,y_a,minute_end_x,minute_end_y)
        e=self.distance(0,0,x_a,y_a)
        alpha_angle=self.alpha(a,o,e)

        minute_shadow_end_x = minute_end_x + k*math.tan(theta-alpha_angle)
        minute_shadow_end_y = minute_end_y + k

        # calculs aiguilles des secondes et ombre
        second_angle = second * math.pi/30 - math.pi/2
        second_end_x = l_sec * w/2 * math.cos(second_angle)
        second_end_y = l_sec * h/2 * math.sin(second_angle)
        second_start_x = -0.28 * w/2 * math.cos(second_angle)
        second_start_y = -0.28 * h/2 * math.sin(second_angle)

        ap=self.distance(0,0,second_start_x,second_start_y)
        op=self.distance(x_a,y_a,second_start_x,second_start_y)
        sp=self.distance(0,0,x_a,y_a)
        alpha_anglep=self.alpha(ap,sp,op)

        second_shadow_start_x = second_start_x + k*math.tan(theta-alpha_anglep)
        second_shadow_start_y = second_start_y + k
        a=self.distance(0,0,second_end_x,second_end_y)
        o=self.distance(x_a,y_a,second_end_x,second_end_y)
        e=self.distance(0,0,x_a,y_a)
        alpha_angle=self.alpha(a,o,e)

        second_shadow_end_x = second_end_x + k*math.tan(theta-alpha_angle)
        second_shadow_end_y = second_end_y + k

        # tracé des ombres
        cr.set_line_cap(cairo.LINE_CAP_ROUND)

        cr.set_source_rgb(*c_shadow)
        cr.move_to(hour_shadow_start_x, hour_shadow_start_y)
        cr.line_to(hour_shadow_end_x, hour_shadow_end_y)
        cr.set_line_width(w_hour*(1+k/y_a))
        cr.stroke()

        cr.set_source_rgb(*c_shadow)
        cr.move_to(minute_shadow_start_x, minute_shadow_start_y)
        cr.line_to(minute_shadow_end_x, minute_shadow_end_y)
        cr.set_line_width(w_minute*(1+k/y_a))
        cr.stroke()

        cr.set_source_rgb(*c_shadow)
        cr.move_to(second_shadow_start_x, second_shadow_start_y)
        cr.line_to(second_shadow_end_x, second_shadow_end_y)
        cr.set_line_width(w_second*(1+k/y_a))
        cr.stroke()

        # tracé des graduations
        cr.set_line_cap(cairo.LINE_CAP_BUTT)
        for i in range(60):

            angle = i * math.pi/30 - math.pi/2
            x2 = 1 * w/2 * math.cos(angle)
            y2 = 1 * h/2 * math.sin(angle)
            if i % 5 == 0:
                x1 = (1-l_grad_5) * w/2 * math.cos(angle)
                y1 = (1-l_grad_5) * h/2 * math.sin(angle)
                cr.set_source_rgb(*c_grad_5)
                cr.move_to(x1, y1)
                cr.line_to(x2, y2)
                cr.set_line_width(w_grad_5)
                cr.stroke()
            else:
                x1 = (1-l_grad) * w/2 * math.cos(angle)
                y1 = (1-l_grad) * h/2 * math.sin(angle)
                cr.set_source_rgb(*c_grad)
                cr.move_to(x1, y1)
                cr.line_to(x2, y2)
                cr.set_line_width(w_grad)
                cr.stroke()


        # tracé des  aiguilles        
        cr.set_line_cap(cairo.LINE_CAP_ROUND)

        cr.set_source_rgb(*c_minute)
        cr.move_to(hour_start_x, hour_start_y)
        cr.line_to(hour_end_x, hour_end_y)
        cr.set_line_width(w_hour)
        cr.stroke()

        cr.set_source_rgb(*c_minute)
        cr.move_to(minute_start_x, minute_start_y)
        cr.line_to(minute_end_x, minute_end_y)
        cr.set_line_width(w_minute)
        cr.stroke()

        cr.set_source_rgb(*c_second)
        cr.move_to(second_start_x, second_start_y)
        cr.line_to(second_end_x, second_end_y)
        cr.set_line_width(w_second)
        cr.stroke()

        # tracé petit disque rouge au centre des aiguilles
        cr.arc(0, 0, r/40, 0, 2*math.pi)
        cr.fill()
        cr.stroke()

        # tracé filet autour de la fenêtre
        cr.set_source_rgb(0.8,0.8,0.8)
        cr.move_to(-w/2, +h/2)
        cr.line_to(-w/2, -h/2)
        cr.line_to(w/2, -h/2)
        cr.set_line_width(2)
        cr.stroke()
        cr.set_source_rgb(0.2,0.2,0.2)
        cr.move_to(-w/2, +h/2)
        cr.line_to(+w/2, +h/2)
        cr.line_to(+w/2, -h/2)
        cr.set_line_width(1)
        cr.stroke()


# ============================================================
# boucle principale

win = Clock()
win.connect("destroy", Gtk.main_quit)
win.show_all()

Gtk.main()

C'est le quatrième article consacré à la programmation Python, GTK et PyGObject. Les trois premiers :

• Exemple minimal PyGObject et Cairo : animation d'une ligne
• Exemple minimal PyGObject et Cairo : tracé d'une ligne
• Exemple minimal PyGObject : mise-à-jour d'une étiquette